MATEMATICA
La matemática es la ciencia deductiva que se dedica al estudio de las propiedades de los entes abstractos y de sus relaciones. Esto quiere decir que las matemáticas trabajan con números, símbolos, figuras geométricas, etc.
A partir de axiomas y siguiendo razonamientos lógicos, las matemáticas analizan estructuras, magnitudes y vínculos de los entes abstractos. Esto permite, una vez detectados ciertos patrones, formular conjeturas y establecer definiciones a las que se llegan por deducción.

Las matemáticas trabajan con cantidades (números) pero también con construcciones abstractas no cuantitativas. Su finalidad es práctica, ya que las abstracciones y los razonamientos lógicos pueden aplicarse en modelos que permiten desarrollar cálculos, cuentas y mediciones con correlato físico.
En matemática, definición, en términos generales, es delimitar, o sea, indicar, expresar el límite que separa un objeto de todos los demás.1 Los pilares estructurales de la matemática son: la definición, el teorema y la demostración matemática. Las definiciones señalan con precisión los conceptos de importancia en la teoría. Los teoremas ( o proposiciones) expresan exactamente lo que hay de verdadero en esos conceptos y las demostraciones revelan, en forma contundente, la verdad de esas afirmaciones.2
Los objetos matemáticos existen mediante definiciones. Por ejemplo, un número puede ser un natural y se llama número compuesto o número primo, par o impar, siempre que cumpla condiciones precisas y específicas. Estas condiciones específicas son la definición del concepto.
Si la función real
 tiene límite matemático
tiene límite matemático  en
en  podemos decir de manera informal que la función
podemos decir de manera informal que la función  tiende hacia el límite
tiende hacia el límite  cerca de
cerca de  si se puede hacer que
si se puede hacer que  esté tan cerca como queramos de
esté tan cerca como queramos de  haciendo que
haciendo que  esté suficientemente cerca de
esté suficientemente cerca de  siendo
siendo  distinto de
distinto de  .
.Los conceptos cerca y suficientemente cerca son matemáticamente poco precisos. Por esta razón, se da una definición formal de límite que precisa estos conceptos. Entonces se dice:
El límite de una función f(x), cuando x tiende a c es L si y sólo si para todo |
A partir de la definición de límite, la derivada de una función f(x) en el punto x es
 donde x ∈ (a,b) ⊂ Df4
donde x ∈ (a,b) ⊂ Df4
Álgebra abstracta
En álgebra abstracta pueden definirse estructuras algebraicas, por ejemplo:Un grupo
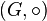 es un conjunto G en el que se ha definido una operación binaria interna
es un conjunto G en el que se ha definido una operación binaria interna  , que satisface las siguientes propiedades o axiomas:5
, que satisface las siguientes propiedades o axiomas:5Por lo tanto, un grupo está formado por un conjunto de elementos abstractos o símbolos, y por una ley de composición interna (operación binaria) que los relaciona. Dicha ley de composición interna indica cómo deben ser manipulados los elementos del grupo.
En este enunciado el elemento simétrico es una definición de inverso multiplicativo en teoría de grupos.
Conceptos no definidos
En un estudio es importante que los términos sean definidos.¿Todos? Pues la pretensión de definir a todos ellos llevaría a un círculo vicioso. Así, p. ej., un diccionario puede definir existir como ser, y en seguida definir ser como existir, con el resultado de que existir significa existir. Para superar esta complicación en un sistema axiomático se eligen ciertos conceptos como conceptos primitivos o conceptos no definidos, y se definen a partir de ellos todas las demás nociones requeridas( peculiaridades de la materia).6Véase también
La etimología de la palabra ‘matemática’ remite al griego, en el que significaba ‘conocimiento’. Se define como la ciencia formal y exacta que, basada en los principios de la lógica, estudia las propiedades y las relaciones que se establecen entre los entes abstractos. Este concepto de ‘entes abstractos’ incluye a los números, los símbolos y las figuras geométricas, entre otros. El campo de estudio de la matemática fue modificándose con el tiempo: hasta el siglo XIX se limitaba al estudio de las cantidades y de los espacios, pero con los avances científicos fueron apareciendo campos de la matemática que excedían esos dos, lo que exigió su redefinición.
La matemática tiene mucha relación con otras ciencias. En primer lugar, se apoya principalmente en la lógica y en sus estrategias para la demostración y la inferencia. Es por esto que la matemática es una ciencia objetiva: solo podrá ser modificada al demostrarse la existencia de errores matemáticos, para lo cual seguramente deberá modificarse gran parte del paradigma científico con el que se trabaja. El método entonces radica en analizar esos entes abstractos para producir hipótesis y conjeturas, realizar deducciones, y acercarse así al conocimiento matemático, que como se ha dicho, se asume exacto y verdadero. Esas deducciones se llevan a cabo con el apoyo de definiciones (limitaciones de algo respecto de todo lo demás) y axiomas (premisas aceptadas sin la necesidad de una demostración).
La aplicación de las matemáticas aparece en casi todos los ámbitos de la vida. Veamos una pequeña reseña:
- En la vida cotidiana, donde con gran asiduidad se hacen cálculos matemáticos, o bien mediciones y comparaciones. Tan omnipresente es la matemática en nuestra vida que muchos expertos consideran a la ausencia de nociones matemáticas como una variante del analfabetismo.
- En las ciencias exactas y naturales. En muchos casos (como la ingeniería o la física), su existencia misma se debe de al enfoque que aportan las matemáticas. En la biología o la química también es sumamente importante la matemática.
- En las ciencias sociales, como la economía o la psicología, que se apoyan en conceptos matemáticos.
- Incluso en otras disciplinas y en las artes (música, escultura, dibujo), se han utilizado y se utilizan recursos matemáticos.
- Aritmética: comprende el estudio de los números. Además de los números naturales, incluye a todos los números racionales, reales y complejos. Las operaciones que se realizan con estos números están incluidas en esta rama.
- Geometría: comprende el estudio de las figuras y sus vínculos con el espacio. Incluye a la trigonometría y a la geometría descriptiva, entre otras.
- Probabilidad y estadística: comprende el análisis de las tendencias sobre la base de un muestreo; resulta de mucho interés para las ciencias sociales.
- Álgebra: es la rama que se dedica a analizar las estructuras, realizando las operaciones aritméticas a través de letras o símbolos.
Derechos Reservados
© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.
Lee todo en: Concepto de matemáticas. Qué es, Significado y Definición. http://concepto.de/matematicas/#ixzz3YciWN0JX
Mediante la abstracción y el uso de la lógica en el razonamiento, las matemáticas han evolucionado basándose en las cuentas, el cálculo y las mediciones, junto con el estudio sistemático de la forma y el movimiento de los objetos físicos. Las matemáticas, desde sus comienzos, han tenido un fin práctico.
Las explicaciones que se apoyaban en la lógica aparecieron por primera vez con la matemática helénica, especialmente con los Elementos de Euclides. Las matemáticas siguieron desarrollándose, con continuas interrupciones, hasta que en el Renacimiento las innovaciones matemáticas interactuaron con los nuevos descubrimientos científicos. Como consecuencia, hubo una aceleración en la investigación que continúa hasta la actualidad.
Hoy en día, las matemáticas se usan en todo el mundo como una herramienta esencial en muchos campos, entre los que se encuentran las ciencias naturales, la ingeniería, la medicina y las ciencias sociales, e incluso disciplinas que, aparentemente, no están vinculadas con ella, como la música (por ejemplo, en cuestiones de resonancia armónica). Las matemáticas aplicadas, rama de las matemáticas destinada a la aplicación de los conocimientos matemáticos a otros ámbitos, inspiran y hacen uso de los nuevos descubrimientos matemáticos y, en ocasiones, conducen al desarrollo de nuevas disciplinas. Los matemáticos también participan en las matemáticas puras, sin tener en cuenta la aplicación de esta ciencia, aunque las aplicaciones prácticas de las matemáticas puras suelen ser descubiertas con el paso del tiempo.
 existe un
existe un 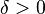 tal que para todo número real x en el dominio de la función
tal que para todo número real x en el dominio de la función  .
.



